V. Coq proof assistant

2. Equational Logic

"Equality (=)" is the binary relation used to define programs and share the same property of the "paths" example (reflexivity, transitivity + rewrite, simplification & induction).
So, all the concepts from proof theory can be applied to (functional) programs !

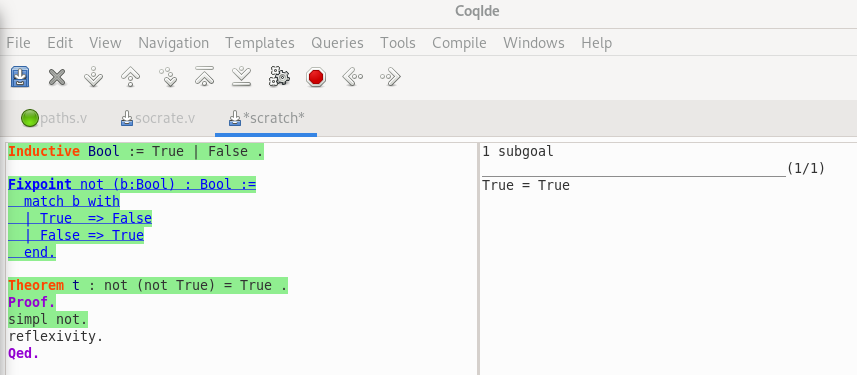
source

Exercise

• Try to prove that: forall b:Bool, not (not b) = b.
• Define the and operator and prove it is "commutate" and "associative".

Languages' equivalences

• Coq = F#
• Inductive = type
• Fixpoint = let rec

3 - 7